 16 logic operations?
16 logic operations? 16 logic operations?
16 logic operations?
Jan Punter said:
A full set of logic function, i.e. all possible 16 logic operations on two inputs (to one output), not just and, or, xor.
Kofi Busia wrote:
What are these, please?
Mountain Man wrote:
Jan's talking about all possible "truth tables", where a truth table specifies for each combinations of inputs, what the output is. For two inputs, there are 4 possible combinations of two inputs - (0,0), (0,1), (1,0), (1,1) - thus the truth table has 4 rows. The table for "And" is:
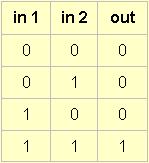

James Clark wrote:
He's talking about a lookup-table (LUT). There are 2^2^N possible Boolean single output functions having N inputs.
For N=2, (say inputs a and b) the 16 possible functions are:

Jan Punter wrote:
Not all do have a 'real' name - but not all things without a name areuseless. Some common names are nand, nor, exnor. Some operators are'collapsed' like 'always 0' or 'always 1', 'straight through'. Invert isanother case of a partially degenerated function, but there is use for thatone. So now we have 10, the other six are created by ading an invertor to oneof the inputs of (and, or, xor). These could be named as (A and not B) etc.
A logic function can be described by its truth table. For 2 inputs a truth table has 4 rows, one row for each of the 4 possible outcomes of a logicfunction on 2 inputs. As there are 4 output values, there are 16 distinctoutput columns possible. These represent the16 distinct functions, oroperators.
For example the truth table of the and function looks like:
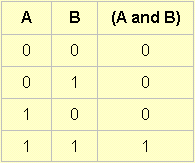
But the possible right hand column's (laid out flat, for ease of typing) are ( 0 0 0 0, 0 0 0 1, ... , 1 1 1 1), 16 in total, as said before.
More on the subject:
Having all logic functions available in one module would ease building control structures. It is true of course that (and, or, xor, not) makes a (over) complete boolean system, but sometimes a lot of logic modules are needed now to accomplish something simple. Four of the operators are really useless (0,1, A,B), but a straighton compact implementation would give those for free.
The next two already are availble (not A, not B) as the Logic Inverter module.
The next three (and, or, xor) are implemented by the logic processor. Which leaves us with seven others that now need two or three modules to implement them - I'd like to have those seven really, but I somehow believe in complete (mathematically pure) systems. The logic inverter module would be obsolete now - which would save an opcode (only 127 are available now, most already in use) for a newly to be invented type of module.
Aside from this:
A multi input and module with switchable inversion on the output would be usefull as well. The or function can be done by the 8 input mixer module (which could use an inverter button on it's output as well).
Jan Punter wrote:
> Mountain Man wrote: Personally, I'd prefer to see a few of the most common (or, and, xor would be enough for me) implemented for more inputs - 8 would be nice, with a "not" button for each input.
I could live with that. It would be easier to understand, would leave out the useless functions, would solve the naming problem, yeah, I could live with that. But it really needs the invertable inputs!
Friday's Child wrote:
Hmmm...... Thanks Mr. Mountain Man. Things are slowly coming back to me. But ... it's really really been a long while since I did this stuff.
So I'm afraid that I still don't quite get it from your explanation. (Sorry!!) What I do now remember is some stuff from classical logic. I used to be a very naughty boy at school and so to punish me they made me do that stuff. In that kind of logic there are four cases for which you could derive a truth table.
(1)
p.q; (2) p v q; (3) p -> q; (4) ~p.Case 1:
p.q
is p and q. With respect to two inputs you have clarified this. I can the four options this gives us. The truth table, if incorporated into a module, would say: "only provide an output when there is an input to both 1 and 2". You already kindly gave the truth table for this, so I repeat it just to be complete.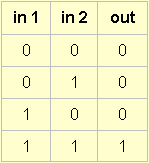
Case 2:
p v q
which is p or q. Again, when you have two inputs, the truth table would I think be: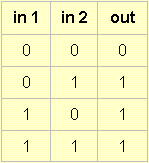
So what the module would do is provide us with an output whenever either 1 or 2 or both had an input.
Case 3:
p -> q
This one is a bit trickier! When talking about sounds, oscillators and modules, probably the best way to interpret it would be something along the lines of: let input 1 be of some specified kind and let the input at 2 be of some other specified kind. You then have to deal with all the four cases in which the two inputs either are or are not of the kind specified.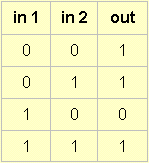
So, by the first row, when neither input is of the specified kind, then you get a specified out. By the second row, if the first is not as specified but the second is ... then you again get an out. The third row tells us: if in 1 is as specified but in 2 is not, then no output. And the final row tells us if both inputs are as specified then please provide an out.
Case 4:
This is presumably where the x-or comes from?
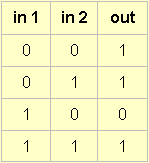
Now that you have jogged my memory enough I have remembered those logical whatever's, and I can get to 16. To be honest, however, I still don't quite understand this explanation you gave:
> since there are 4 rows, there are 2 to 4th power = 16 possible sets of output (note that the input columns are the same for all truth tables).
I don't get how you extrapolate from 4 rows to give 16 possible types. I dredged the other three logical operations up from my memory and using those, I was able to get to 16. Is that what you meant? I am not clear about it because all you ever mentioned was the 'and' operation. Is there some other way of getting to 16 using those 'and' types? If so, what is it? Or ... did I do the right thing in suddenly remembering those other operations? In which case, I still don't quite see how 16 is made because the fact that there are 4 logical operations is surely distinct from the 2^4 you mentioned.
> Personally, I'd prefer to see a few of the most common (or, and, xor would be enough for me) implemented for more inputs - 8 would be nice, with a "not" button for each input.
Well ... I'm not quite so sure about this!! The p -> q structure, for example, has some nice possibilities. What 16-fold logical module could do, perhaps, is allow you to pass on the results of its calculation to another one of the same type? Alternatively ... you could have the eight in's you have mentioned, and then be able to team any two of them up in any logical operation you wanted?!!!
As for my question ... sorry if I seem to be being a bit dim ... but like I said, it's been a while!
Carbon111 wrote:
Friday's Child wrote:
> Friday's Child said: To be honest, however, I still don't quite understand this explanation...
> Jan Punter then said: A logic function can be described by its truth table. <snip> As there are 4 output values, there are 16 distinct output columns possible. These represent the16 distinct functions, or operators. <snip> But the possible right hand column's (laid out flat, for ease of typing) are ( 0 0 0 0, 0 0 0 1, ... , 1 1 1 1), 16 in total, as said before.
Got it. Subject closed. Thanks to you both. Sorry Mr. Mountain Man ... now I think about it ... you were perfectly clear! Next time I will do better.
Mountain Man wrote:
You're right, Kofi, my explanation of "2 to the fourth" was a bit dense, I'll try again, not sure if I'll be any clearer!
What I was getting at is that only the output column (3rd column) changes. I'll write the result from each row as an entry in a vector, one position in the vector per row of the truth table. Your first example below would be represented by (0,0,0,1). Now, you can imagine values of this vector running from (0,0,0,0) meaning that no matter what the value of p and the value of q, the output value is always 0. I think Jan called this "always 0 ! The other end of the spectrum is all output 1 - (1,1,1,1). In between are other combinations - "and" is (0,0,0,1), "or" is (0,1,1,1), etc. As Jan noted, some have names (btw, "xor" is (0,1,1,0)), and some don't. Since there are 4 elements in the "result vector", and two possible values at each position, there are 16 combinations. Did I confuse you in a new way now?
Friday's Child wrote:
Hi James Clark,
Nice to hear from you. Things gets better and better. Thank you very much.
One last REALLY REALLY STUPID question. OK? (Well ... I hope it's the last one! I'm not promising anything, though.)
If '!' is a negation ... then what on earth do the '1' and the '0' at the beginning of this little list mean? Do they mean 'presence of' and 'absence of' ... or what? If so, then how do they differ from just 'a' and 'b' ... or would it kind of mean 'it's irrelevant which one, as long as at least one is there". Or ... am I completely off the wall there? Maybe ... that 1 and 0 don't have any 'real' representation?
OK ... I have a second really stupid question. Do all these 16 functions have names? Jan Punter hinted that they didn't and I'm inclined to believe him ... but just because he doesn't know doesn't mean that there aren't any. (No offence, Jan!!)
Thanks. I'm grateful. Can't see the point, actually, in me learning all this, or what difference knowing it is going to make to my boring little life ... but I'd kind of like to learn it anyway.
Friday's Child wrote:
Hi Mr. Mountain Man Elby Sir,
I'm a-gettin' there. Yes, what you said made sense. I now know enough to know that I got 'xor' completely the wrong way round.
> Since there are 4 elements in the "result vector", and two possible values at each position, there are 16 combinations.
Got it.
> Did I confuse you in a new way now?
Well ... I won't answer that on the grounds that it might incriminate me. Anyway, I'm kind of enjoying this!
I really do have an extremely warped sense of fun!!!!!
It's really lucky for me you guys are all so tolerant. Thanks.
Friday's Child wrote:
OK. I am sorry to Mountain Man, James Clark and Jan Punter for having so very dense about this, but I think I honestly think I have got it now!
Let there be two objects (say A and B) in each of which it is possible to distinguish two states (e.g. on/off or 0/1). Let those two objects now be combined and taken in pairs. With those two states there are 4 and only four possibilities:

The name for this state can be 'always 0'.
2. No matter what happens amongst the inputs, let there ALWAYS be an output:
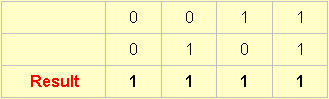
And the name for this state can be 'always 1'.
3. There are then four sets of states that share the similarity that there is only one amongst the four combinations ever produces an output. These all involve some kind of an 'and' condition and are as follows:
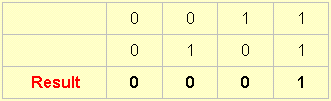
Here we only get an output when A AND B are both present -- or when both inputs are producing.
4. The other three states in this set are some variation of 'and'.
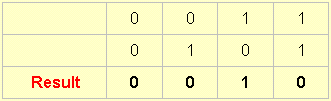
This one is called A and not-B.
5.
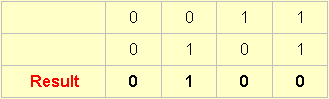
6.
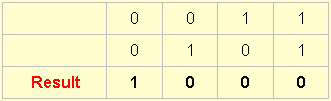
And this one is called not-A and not-B.
Similarly, there is a set of four similar states in which we can have an output on three occasions:
7.
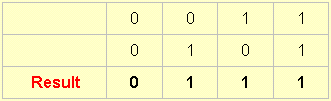
This one can be called: A or B.
The other three in this set are also some kind of 'or'.
8.
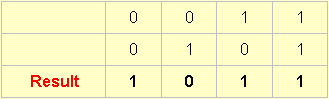
This one is A or not-B
9.
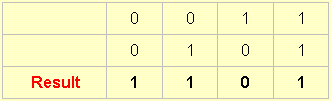
This one is called not-A or B
10.
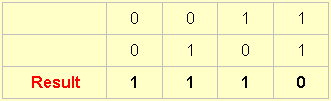
And this one is called not-A or not-B
The last remaining set of 6 states all give an output on 2 occasions.
11.
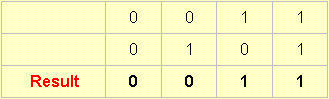
This one is produced by accepting an output whenever A is present, and1refusing it otherwise.
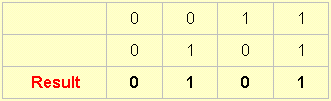
And this one is produced by accepting an output whenever B is present, and refusing it otherwise.
13.
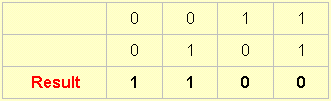
This one results by accepting an output whenever A is absent.
14.
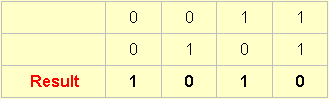
And this one results by accepting an output whenever B is absent.
And ... finally ... the last two are the exclusive or's or xor's.
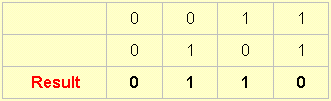
This results by accepting an output whenever the two objects are in different conditions, and refusing it whenever they are the same. Hence .. exclusive or.
16.
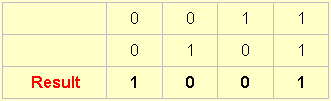
And, finally, this is the complement of the exclusive or immediately above and arises by accepting an output whenever we have either a not-A or a B, but not both.
And that completes the set.
And ... what a thorough waste of time THAT was to be sure. Why on earth would any normal person want to puzzle over it? But ... at least I understand it now. Or ... I hope I do.
If it is wrong, then please someone who knows better let me know where it is wrong and why. And ... sorry James for having posed to you such a LUDICROUSLY stupid question as asking you for their 'names'. You must have thought I was two planks short of a full wheelbarrow or something. Thanks, though, to you, Jan and Mountain Man for helping me see the light. I have seen the light. Praise be!!!
Mountain Man wrote:
You're getting warm, Kofi J *Most* of what you said was correct - except, of course, for the fact that "A" and "B" are always represented as columns, not as rows! <g>, and a name or two that's not right. Beyond that, I'll add some information - I pulled a book off the shelf, and have some names for you.
The names of the 16 items you present are:
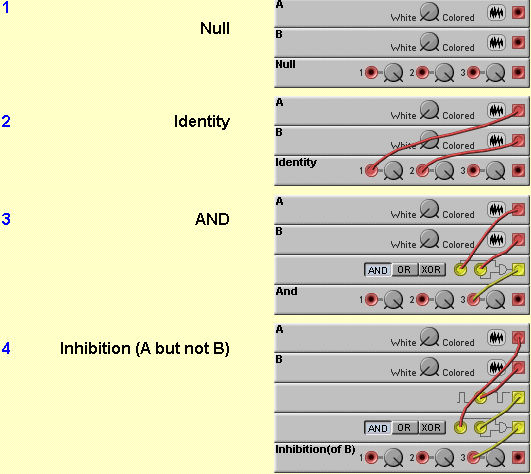
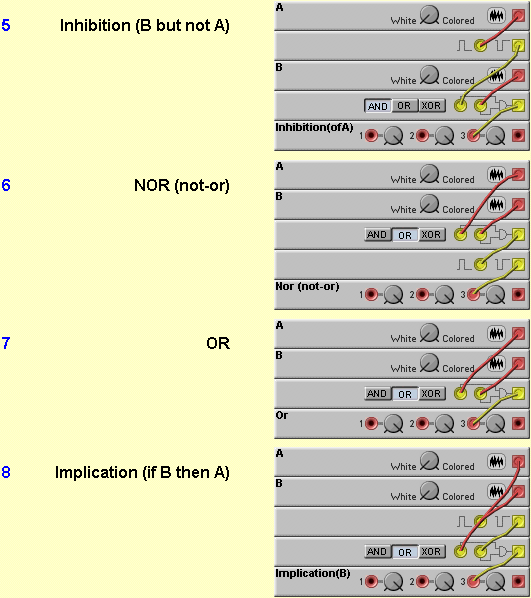
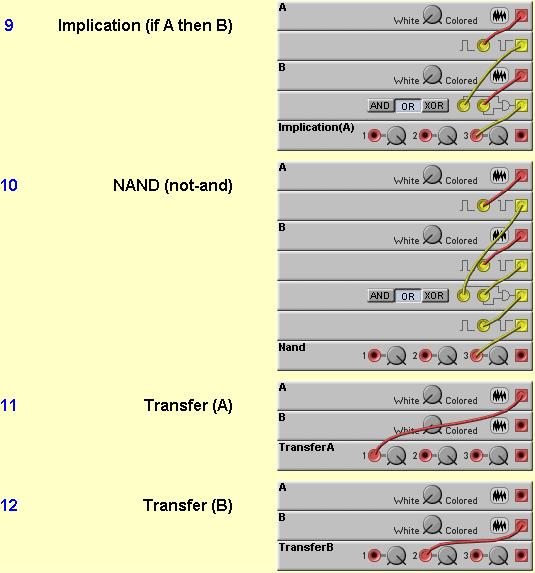

BTW, the typical ordering of these (or anything that involves binary enumeration) is to start with (0,0,0,0) then (0,0,0,1), (0,0,1,0), (0,0,1,1)... in order of binary counting. Notice a couple of interesting facts. ~(A OR B) = ~A AND ~B (~ represents "not") Also, ~(A AND B) = ~A OR ~B. You seem to understand this :) These are called DeMorgan's laws, and are very important for transforming logic function - mostly to simplify them (mostly used for logic functions that take more than 2 inputs). I'll probably write some more about simplifying logic functions (assuming you're interested <g>), but I need to go to work now!
Friday's Child wrote:
> Mountain Man wrote: BTW, the typical ordering of these (or anything that involves binary enumeration) is to start with (0,0,0,0) then (0,0,0,1), (0,0,1,0), (0,0,1,1) ... in order of binary counting.
Go down the columns in the attached patch. I hope I wired them all up right! They all actually look quite interesting. Gives you the opportunity to patch things up in a whole load of different ways and with different control options.
Eg, by slapping in a compare and a tuning module, you could get different tunings in different contexts etc according to a whole load of different
switching conditions of velocity, pitch, filtering etc. Or ... the transfer module could be used to pass a signal straight through under some conditions, while modifying something else when its velocity increased above a certain point ... but only if .... etc. Must say that I now agree with Jan. Would be very nice to have them all available at the press of a button. Really nice. I am also getting quite mouth-watering reading some of the other things people are praying for in the new OS.
> Notice a couple of interesting facts. ~(A OR B) = ~A AND ~B (~ represents "not") Also, ~(A AND B) = ~A OR ~B. These are called DeMorgan's laws
Ah yes ... DeMorgan.
> I'll probably write some more about simplifying logic functions (assuming you're interested <g>)
You'll probably bore everyone else rigid!!
Hopefully, they are all now present in the attached patch, complete with names, and in 'logical' order!! Thanks very much for them names.
Quite brought my old school/university days right back! You're not my old Aristotelian logic tutor are you? If so ... I have a bone to pick with you!!!