| Author |
Message |
jazzmonster
Joined: Jun 29, 2014
Posts: 6
Location: Dublin, Ireland
|
 Posted: Sun Jun 29, 2014 7:28 am Post subject:
Euclidean generator in ChucK |
  |
|
Hi, I'm interested in using ChucK for live performance. I only started learning it a few days ago. I do have some general programming experience.
I'm trying to put together a simple Euclidean sequence generator. Here's what I'm talking about:
https://web.archive.org/web/20131114124454/http://ruinwesen.com/blog?id=216
Theoretical background:
https://web.archive.org/web/20131204032416/http://cgm.cs.mcgill.ca/~godfried/publications/banff.pdf
Existing implementation in Java:
http://kreese.net/blog/2010/03/27/generating-musical-rhythms/#tb
As far as I understand Chuck lacks array operations like sorting or concatenating etc. (correct me if I'm wrong) which makes it quite difficult. I came across this post:
http://blog.noizeramp.com/2008/10/26/rhythm-generation-with-an-euclidian-algorithm/
It's a ruby algorithm which uses simple mathematical formula to generate the euclidean sequence, as opposed to the Bjorklund's algorithm (sorting arrays) described in the articles above.
I adapted it for ChucK.
| Code: |
fun int[] euclideangenerator ( int pulses, int steps ) {
// pulses - amount of pulses
// steps - amount of discrete timing intervals
steps - pulses => int pauses;
pauses / pulses $ int => int per_pulse;
pauses % pulses => int remainder;
int seq[steps];
int step;
for ( int i; i < pulses; i++ ) {
true => seq[step];
step++;
for ( int j; j < per_pulse; j++) {
false => seq[step];
step++;
}
if ( i < remainder ) {
false => seq[step];
step++;
}
}
return seq;
}
|
It generally works well and generates very interesting sequences.
The simple ruby algorithm (and therefore my implementation in ChucK) seem to be flawed though and in certain conditions it generates an incorrect output (still very interesting but not an euclidean sequence).
For example for (7,12) , i.e. 7 pulses and 12 steps, my algorithm (and ruby code) generates:
[ 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1 ]
whereas the correct euclidean sequence (as per Godfried Toussaint's PDF above) is:
[ 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0 ]
I would like to ask 2 questions:
1. Are there any obvious mistakes in my implementation (and the original ruby code) or is it just not possible to generate a correct euclidean sequence without using the Bjorklund's algorithm? If so:
2. Does anyone know how to implement the Bjorklund's algorithm in ChucK?
Could any of the more experienced ChucK users help me with the above?
Thanks
_________________
jazzmonster |
|
|
Back to top
|
|
 |
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Sun Jun 29, 2014 8:11 am Post subject:
|
|
|
 jazzmonster
I don't understand the algorithm ... the variable step seems to be not initialized and would go out of the sequence array bounds?
Apart from that, yes your program gives a result where three ones are in a row (looking at it as a circle) so that can not be right.
_________________
Jan
also .. could someone please turn down the thermostat a bit.
 |
|
|
Back to top
|
|
|
Antimon
Joined: Jan 18, 2005
Posts: 4145
Location: Sweden
Audio files: 371
G2 patch files: 100
|
| Posted: Sun Jun 29, 2014 9:00 am Post subject:
|
|
|
jazzmonster
One thing I can see is that in your example (7, 12), the per_pulse variable will be set to zero, meaning that the for-loop using j as iteration variable will never run.
_________________
Antimon's Window
@soundcloud @Flattr home - you can't explain music |
|
|
Back to top
|
|
|
jazzmonster
Joined: Jun 29, 2014
Posts: 6
Location: Dublin, Ireland
|
| Posted: Sun Jun 29, 2014 9:06 am Post subject:
|
|
|
Hi guys,
@Blue Hell - steps variable does stay within array bounds, so the problem doesn't lay there
@Antimon - Well spotted. So this seems to be the problem with the algorithm. Whenever ( pulses >= pauses ), per_pulse variable is zero and hence the incorrect output. I wonder is there a way of fixing this?
_________________
jazzmonster |
|
|
Back to top
|
|
|
Antimon
Joined: Jan 18, 2005
Posts: 4145
Location: Sweden
Audio files: 371
G2 patch files: 100
|
| Posted: Sun Jun 29, 2014 9:56 am Post subject:
|
|
|
One way might be to keep per_pulse floating point, add an extra floating point variable (pulse_accumulator in my dry coding below) that you add to in each iteration over i, and then instead of the loop over j do something like:
| Code: |
per_pulse +=> pulse_accumulator;
while (pulse_accumulator > 1.0) {
false => seq[step++];
1.0 -=> pulse_accumulator;
}
|
_________________
Antimon's Window
@soundcloud @Flattr home - you can't explain music |
|
|
Back to top
|
|
|
Antimon
Joined: Jan 18, 2005
Posts: 4145
Location: Sweden
Audio files: 371
G2 patch files: 100
|
| Posted: Sun Jun 29, 2014 9:59 am Post subject:
|
|
|
| Blue Hell wrote: | :welcome: jazzmonster
I don't understand the algorithm ... the variable step seems to be not initialized and would go out of the sequence array bounds?
Apart from that, yes your program gives a result where three ones are in a row (looking at it as a circle) so that can not be right. |
The default value for numeric variables is zero, which is also used in the for loop initalizers - I haven't seen that kind of code before, nice. :)
I've always written
| Code: | for (0 => int i; i < count; i++) {
...
} |
but it seems that this works just as well:
| Code: | for (int i; i < count; i++) {
...
} |
since the i variable is defined inside the for loop and undefined outside.
_________________
Antimon's Window
@soundcloud @Flattr home - you can't explain music |
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Sun Jun 29, 2014 11:38 am Post subject:
|
|
|
Ah ok, yeah, zero initialized .. had inferred that for the for loops but not for the step variable .. lol.
_________________
Jan
also .. could someone please turn down the thermostat a bit.
|
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Sun Jun 29, 2014 11:50 am Post subject:
|
|
|
FWIW ... I made a totally different implementation (for the Nord Modular G2) based on two LFOs and a D FlipFlop.
The post about it is here
And it looks like
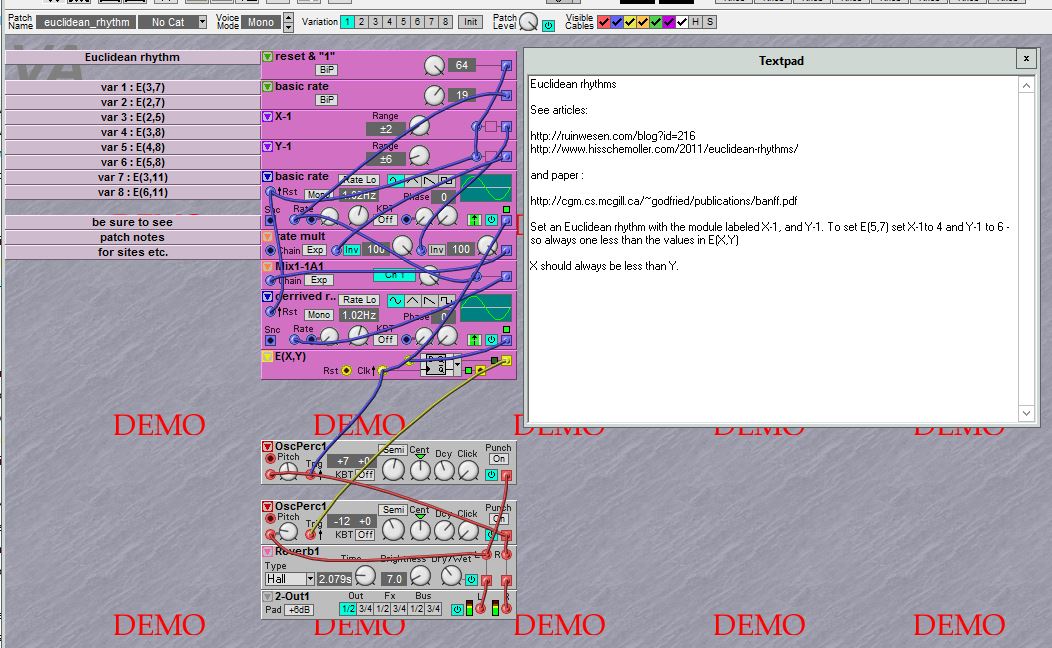
in the G2 demo program.
_________________
Jan
also .. could someone please turn down the thermostat a bit.
|
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Sun Jun 29, 2014 1:08 pm Post subject:
|
|
|
I just implemented that ChucK algorithm in Pascal ... I get the same issue ... trying to understand why that is now ...
| Code: | procedure TMainForm.TestStuff;
function Counts( S: string): string;
var
i : Integer;
ones : Integer;
begin
ones := 0;
for i := 1 to Length( S)
do begin
if S[ i] = '1'
then Inc( ones);
end;
Result := Format( '%d steps with %d pulses', [ Length( S), ones]);
end;
const
Steps = 12;
Pulses = 7;
var
Rhythm : string;
Pauses : Integer;
PerPulse : Integer;
Remainder : Integer;
Pulse : Integer;
j : Integer;
begin
Pauses := Steps - Pulses;
PerPulse := Pauses div Pulses;
Remainder := Pauses mod Pulses;
Rhythm := '';
for Pulse := 0 to Pulses - 1
do begin
Rhythm := Rhythm + '1';
for j := 0 to PerPulse - 1
do Rhythm := Rhythm + '0';
if Pulse < Remainder
then Rhythm := Rhythm + '0';
end;
DisplayFmt( 'rhythm: %s [%s]', [ Rhythm, Counts( Rhythm)]);
end;
|
output :
| Code: | | rhythm: 101010101011 [12 steps with 7 pulses] |
_________________
Jan
also .. could someone please turn down the thermostat a bit.
|
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Sun Jun 29, 2014 2:05 pm Post subject:
|
|
|
Ah .. maybe Bresenham can come to the rescue ... http://en.wikipedia.org/wiki/Euclidean_Rhythm points to that
As implemented in Pascal :
| Code: | procedure TMainForm.TestStuff5;
const
Steps = 12;
Pulses = 7;
var
Rhythm : string;
Error : Single;
DError : Single;
i : Integer;
begin
Error := 0;
DError := Pulses / Steps;
for i := 0 to Steps - 1
do begin
Error := Error + DError;
if Error > 0.5
then begin
Rhythm := Rhythm + '1';
Error := Error - 1;
end
else Rhythm := Rhythm + '0';
end;
DisplayFmt( 'rhythm 4: %s [%s]', [ Rhythm, Counts( Rhythm)]);
end;
|
Simplified version:
| Code: |
function EuclideanRhythm2( aPulses, aSteps: Integer): string;
var
Error : Integer;
i : Integer;
begin
Result := '';
if aSteps > 0
then begin
Error := 0;
for i := 0 to aSteps - 1
do begin
Error := Error + aPulses;
if Error >= aSteps div 2
then begin
Result := Result + '1';
Error := Error - aSteps;
end
else Result := Result + '0';
end;
end;
end;
|
This seems to work for a couple of test cases I did ...
| Code: | Euclidean( 1, 2) -> Rhythm: 10
Euclidean( 1, 3) -> Rhythm: 100
Euclidean( 2, 3) -> Rhythm: 110
Euclidean( 1, 4) -> Rhythm: 0100
Euclidean( 2, 4) -> Rhythm: 1010
Euclidean( 3, 4) -> Rhythm: 1101
Euclidean( 1, 5) -> Rhythm: 01000
Euclidean( 2, 5) -> Rhythm: 10010
Euclidean( 3, 5) -> Rhythm: 10110
Euclidean( 4, 5) -> Rhythm: 11101
Euclidean( 1, 6) -> Rhythm: 001000
Euclidean( 2, 6) -> Rhythm: 010010
Euclidean( 3, 6) -> Rhythm: 101010
Euclidean( 4, 6) -> Rhythm: 101101
Euclidean( 5, 6) -> Rhythm: 111011
Euclidean( 1, 7) -> Rhythm: 0010000
Euclidean( 2, 7) -> Rhythm: 0100100
Euclidean( 3, 7) -> Rhythm: 1001010
Euclidean( 4, 7) -> Rhythm: 1010110
Euclidean( 5, 7) -> Rhythm: 1101101
Euclidean( 6, 7) -> Rhythm: 1111011
Euclidean( 1, 8) -> Rhythm: 00010000
Euclidean( 2, 8) -> Rhythm: 01000100
Euclidean( 3, 8) -> Rhythm: 01010010
Euclidean( 4, 8) -> Rhythm: 10101010
Euclidean( 5, 8) -> Rhythm: 10110101
Euclidean( 6, 8) -> Rhythm: 11011101
Euclidean( 7, 8) -> Rhythm: 11110111
Euclidean( 1, 9) -> Rhythm: 000100000
Euclidean( 2, 9) -> Rhythm: 010000100
Euclidean( 3, 9) -> Rhythm: 010010010
Euclidean( 4, 9) -> Rhythm: 100101010
Euclidean( 5, 9) -> Rhythm: 101010110
Euclidean( 6, 9) -> Rhythm: 101101101
Euclidean( 7, 9) -> Rhythm: 110111101
Euclidean( 8, 9) -> Rhythm: 111110111
Euclidean( 1, 10) -> Rhythm: 0000100000
Euclidean( 2, 10) -> Rhythm: 0010000100
Euclidean( 3, 10) -> Rhythm: 0100100010
Euclidean( 4, 10) -> Rhythm: 0101001010
Euclidean( 5, 10) -> Rhythm: 1010101010
Euclidean( 6, 10) -> Rhythm: 1010110101
Euclidean( 7, 10) -> Rhythm: 1011101101
Euclidean( 8, 10) -> Rhythm: 1101111011
Euclidean( 9, 10) -> Rhythm: 1111101111
Euclidean( 1, 11) -> Rhythm: 00001000000
Euclidean( 2, 11) -> Rhythm: 00100001000
Euclidean( 3, 11) -> Rhythm: 01000100100
Euclidean( 4, 11) -> Rhythm: 01010010010
Euclidean( 5, 11) -> Rhythm: 10010101010
Euclidean( 6, 11) -> Rhythm: 10101010110
Euclidean( 7, 11) -> Rhythm: 10110110101
Euclidean( 8, 11) -> Rhythm: 11011011101
Euclidean( 9, 11) -> Rhythm: 11101111011
Euclidean( 10, 11) -> Rhythm: 11111101111
Euclidean( 1, 12) -> Rhythm: 000001000000
Euclidean( 2, 12) -> Rhythm: 001000001000
Euclidean( 3, 12) -> Rhythm: 010001000100
Euclidean( 4, 12) -> Rhythm: 010010010010
Euclidean( 5, 12) -> Rhythm: 010101001010
Euclidean( 6, 12) -> Rhythm: 101010101010
Euclidean( 7, 12) -> Rhythm: 101011010101
Euclidean( 8, 12) -> Rhythm: 101101101101
Euclidean( 9, 12) -> Rhythm: 110111011101
Euclidean( 10, 12) -> Rhythm: 111011111011
Euclidean( 11, 12) -> Rhythm: 111111011111
Euclidean( 1, 13) -> Rhythm: 0000010000000
Euclidean( 2, 13) -> Rhythm: 0010000001000
Euclidean( 3, 13) -> Rhythm: 0100001000100
Euclidean( 4, 13) -> Rhythm: 0100100100010
Euclidean( 5, 13) -> Rhythm: 0101001010010
Euclidean( 6, 13) -> Rhythm: 1001010101010
Euclidean( 7, 13) -> Rhythm: 1010101010110
Euclidean( 8, 13) -> Rhythm: 1011010110101
Euclidean( 9, 13) -> Rhythm: 1011101101101
Euclidean( 10, 13) -> Rhythm: 1101110111101
Euclidean( 11, 13) -> Rhythm: 1110111111011
Euclidean( 12, 13) -> Rhythm: 1111111011111
Euclidean( 1, 14) -> Rhythm: 00000010000000
Euclidean( 2, 14) -> Rhythm: 00010000001000
Euclidean( 3, 14) -> Rhythm: 00100010000100
Euclidean( 4, 14) -> Rhythm: 01000100100010
Euclidean( 5, 14) -> Rhythm: 01001010010010
Euclidean( 6, 14) -> Rhythm: 01010100101010
Euclidean( 7, 14) -> Rhythm: 10101010101010
Euclidean( 8, 14) -> Rhythm: 10101011010101
Euclidean( 9, 14) -> Rhythm: 10110110101101
Euclidean( 10, 14) -> Rhythm: 10111011011101
Euclidean( 11, 14) -> Rhythm: 11011110111011
Euclidean( 12, 14) -> Rhythm: 11101111110111
Euclidean( 13, 14) -> Rhythm: 11111110111111
Euclidean( 1, 15) -> Rhythm: 000000100000000
Euclidean( 2, 15) -> Rhythm: 000100000010000
Euclidean( 3, 15) -> Rhythm: 001000010000100
Euclidean( 4, 15) -> Rhythm: 010001000100100
Euclidean( 5, 15) -> Rhythm: 010010010010010
Euclidean( 6, 15) -> Rhythm: 010100101001010
Euclidean( 7, 15) -> Rhythm: 100101010101010
Euclidean( 8, 15) -> Rhythm: 101010101010110
Euclidean( 9, 15) -> Rhythm: 101011010110101
Euclidean( 10, 15) -> Rhythm: 101101101101101
Euclidean( 11, 15) -> Rhythm: 110110111011101
Euclidean( 12, 15) -> Rhythm: 110111101111011
Euclidean( 13, 15) -> Rhythm: 111101111110111
Euclidean( 14, 15) -> Rhythm: 111111110111111
Euclidean( 1, 16) -> Rhythm: 0000000100000000
Euclidean( 2, 16) -> Rhythm: 0001000000010000
Euclidean( 3, 16) -> Rhythm: 0010000100000100
Euclidean( 4, 16) -> Rhythm: 0100010001000100
Euclidean( 5, 16) -> Rhythm: 0100100100010010
Euclidean( 6, 16) -> Rhythm: 0101001001010010
Euclidean( 7, 16) -> Rhythm: 0101010100101010
Euclidean( 8, 16) -> Rhythm: 1010101010101010
Euclidean( 9, 16) -> Rhythm: 1010101101010101
Euclidean( 10, 16) -> Rhythm: 1011010110110101
Euclidean( 11, 16) -> Rhythm: 1011011101101101
Euclidean( 12, 16) -> Rhythm: 1101110111011101
Euclidean( 13, 16) -> Rhythm: 1101111101111011
Euclidean( 14, 16) -> Rhythm: 1111011111110111
Euclidean( 15, 16) -> Rhythm: 1111111101111111
|
_________________
Jan
also .. could someone please turn down the thermostat a bit.
Last edited by blue hell on Sun Jun 29, 2014 3:43 pm; edited 1 time in total |
|
|
Back to top
|
|
|
jazzmonster
Joined: Jun 29, 2014
Posts: 6
Location: Dublin, Ireland
|
| Posted: Sun Jun 29, 2014 3:34 pm Post subject:
|
|
|
| Blue Hell wrote: | Ah .. maybe Bresenham can come to the rescue ... http://en.wikipedia.org/wiki/Euclidean_Rhythm points to that
As implemented in Pascal :
| Code: | procedure TMainForm.TestStuff5;
const
Steps = 12;
Pulses = 7;
var
Rhythm : string;
Error : Single;
DError : Single;
i : Integer;
begin
Error := 0;
DError := Pulses / Steps;
for i := 0 to Steps - 1
do begin
Error := Error + DError;
if Error > 0.5
then begin
Rhythm := Rhythm + '1';
Error := Error - 1;
end
else Rhythm := Rhythm + '0';
end;
DisplayFmt( 'rhythm 4: %s [%s]', [ Rhythm, Counts( Rhythm)]);
end;
|
This seems to work for a couple of test cases I did ... |
Thanks a lot, that's a great find, we seem to be getting closer to solving the problem. I implemented the algorithm in ChucK:
| Code: | fun int[] euclideangenerator ( int pulses, int steps ) {
// Euclidean rhythm generator based Bresenham's algorithm
// pulses - amount of pulses
// steps - amount of discrete timing intervals
int seq[steps];
float error;
( pulses $ float ) / ( steps $ float ) => float derror;
for ( int i; i < steps; i++ ) {
error + derror => error;
if ( error > 0.5 ) {
true => seq[i];
error - 1 => error;
} else {
false => seq[i];
}
}
return seq;
} |
The only issue with it is that most of the patterns are rotated (shifted) compared to the euclidean rhythm examples from the paper in the first post.
For example: (2,7) generates [ 0, 1, 0, 0, 0, 1, 0 ] instead of the correct [ 1, 0, 0, 0, 1, 0, 0 ]. So the above functions result is shifted 1 step to the right.
The shift (rotation) varies per rhythm and I can't seem to be able to figure out any correlation. I am going to do some further reading about Bresenham's algorithm. Also it looks like there is a way of avoiding float type operations.
_________________
jazzmonster |
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Sun Jun 29, 2014 3:47 pm Post subject:
|
|
|
The shifts are not incorrect ... just permutations ... the algorithm just generates one of the possible permutations.
Edit: I posted a 2nd algorithm that needs no floats - in the post above.
_________________
Jan
also .. could someone please turn down the thermostat a bit.
|
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Sun Jun 29, 2014 4:06 pm Post subject:
|
|
|
Ok .. here is a variation that lets patterns start with a 1 always.
| Code: | function EuclideanRhythm3( aPulses, aSteps: Integer): string;
var
Error : Integer;
i : Integer;
begin
Result := '';
if aSteps > 0
then begin
Error := 0;
for i := 0 to aSteps - 1
do begin
Error := Error + aPulses;
if Error > 0
then begin
Result := Result + '1';
Error := Error - aSteps;
end
else Result := Result + '0';
end;
end;
end;
|
_________________
Jan
also .. could someone please turn down the thermostat a bit.
|
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Sun Jun 29, 2014 4:08 pm Post subject:
|
|
|
with results (the ok means that the right number of 1's is present) :
| Code: | Euclidean( 1, 2) -> Rhythm: 10 :: ok
Euclidean( 1, 3) -> Rhythm: 100 :: ok
Euclidean( 2, 3) -> Rhythm: 110 :: ok
Euclidean( 1, 4) -> Rhythm: 1000 :: ok
Euclidean( 2, 4) -> Rhythm: 1010 :: ok
Euclidean( 3, 4) -> Rhythm: 1110 :: ok
Euclidean( 1, 5) -> Rhythm: 10000 :: ok
Euclidean( 2, 5) -> Rhythm: 10100 :: ok
Euclidean( 3, 5) -> Rhythm: 11010 :: ok
Euclidean( 4, 5) -> Rhythm: 11110 :: ok
Euclidean( 1, 6) -> Rhythm: 100000 :: ok
Euclidean( 2, 6) -> Rhythm: 100100 :: ok
Euclidean( 3, 6) -> Rhythm: 101010 :: ok
Euclidean( 4, 6) -> Rhythm: 110110 :: ok
Euclidean( 5, 6) -> Rhythm: 111110 :: ok
Euclidean( 1, 7) -> Rhythm: 1000000 :: ok
Euclidean( 2, 7) -> Rhythm: 1001000 :: ok
Euclidean( 3, 7) -> Rhythm: 1010100 :: ok
Euclidean( 4, 7) -> Rhythm: 1101010 :: ok
Euclidean( 5, 7) -> Rhythm: 1110110 :: ok
Euclidean( 6, 7) -> Rhythm: 1111110 :: ok
Euclidean( 1, 8) -> Rhythm: 10000000 :: ok
Euclidean( 2, 8) -> Rhythm: 10001000 :: ok
Euclidean( 3, 8) -> Rhythm: 10100100 :: ok
Euclidean( 4, 8) -> Rhythm: 10101010 :: ok
Euclidean( 5, 8) -> Rhythm: 11011010 :: ok
Euclidean( 6, 8) -> Rhythm: 11101110 :: ok
Euclidean( 7, 8) -> Rhythm: 11111110 :: ok
Euclidean( 1, 9) -> Rhythm: 100000000 :: ok
Euclidean( 2, 9) -> Rhythm: 100010000 :: ok
Euclidean( 3, 9) -> Rhythm: 100100100 :: ok
Euclidean( 4, 9) -> Rhythm: 101010100 :: ok
Euclidean( 5, 9) -> Rhythm: 110101010 :: ok
Euclidean( 6, 9) -> Rhythm: 110110110 :: ok
Euclidean( 7, 9) -> Rhythm: 111101110 :: ok
Euclidean( 8, 9) -> Rhythm: 111111110 :: ok
Euclidean( 1, 10) -> Rhythm: 1000000000 :: ok
Euclidean( 2, 10) -> Rhythm: 1000010000 :: ok
Euclidean( 3, 10) -> Rhythm: 1001001000 :: ok
Euclidean( 4, 10) -> Rhythm: 1010010100 :: ok
Euclidean( 5, 10) -> Rhythm: 1010101010 :: ok
Euclidean( 6, 10) -> Rhythm: 1101011010 :: ok
Euclidean( 7, 10) -> Rhythm: 1110110110 :: ok
Euclidean( 8, 10) -> Rhythm: 1111011110 :: ok
Euclidean( 9, 10) -> Rhythm: 1111111110 :: ok
Euclidean( 1, 11) -> Rhythm: 10000000000 :: ok
Euclidean( 2, 11) -> Rhythm: 10000100000 :: ok
Euclidean( 3, 11) -> Rhythm: 10010001000 :: ok
Euclidean( 4, 11) -> Rhythm: 10100100100 :: ok
Euclidean( 5, 11) -> Rhythm: 10101010100 :: ok
Euclidean( 6, 11) -> Rhythm: 11010101010 :: ok
Euclidean( 7, 11) -> Rhythm: 11011011010 :: ok
Euclidean( 8, 11) -> Rhythm: 11101110110 :: ok
Euclidean( 9, 11) -> Rhythm: 11111011110 :: ok
Euclidean( 10, 11) -> Rhythm: 11111111110 :: ok
Euclidean( 1, 12) -> Rhythm: 100000000000 :: ok
Euclidean( 2, 12) -> Rhythm: 100000100000 :: ok
Euclidean( 3, 12) -> Rhythm: 100010001000 :: ok
Euclidean( 4, 12) -> Rhythm: 100100100100 :: ok
Euclidean( 5, 12) -> Rhythm: 101010010100 :: ok
Euclidean( 6, 12) -> Rhythm: 101010101010 :: ok
Euclidean( 7, 12) -> Rhythm: 110101101010 :: ok
Euclidean( 8, 12) -> Rhythm: 110110110110 :: ok
Euclidean( 9, 12) -> Rhythm: 111011101110 :: ok
Euclidean( 10, 12) -> Rhythm: 111110111110 :: ok
Euclidean( 11, 12) -> Rhythm: 111111111110 :: ok
Euclidean( 1, 13) -> Rhythm: 1000000000000 :: ok
Euclidean( 2, 13) -> Rhythm: 1000001000000 :: ok
Euclidean( 3, 13) -> Rhythm: 1000100010000 :: ok
Euclidean( 4, 13) -> Rhythm: 1001001001000 :: ok
Euclidean( 5, 13) -> Rhythm: 1010010100100 :: ok
Euclidean( 6, 13) -> Rhythm: 1010101010100 :: ok
Euclidean( 7, 13) -> Rhythm: 1101010101010 :: ok
Euclidean( 8, 13) -> Rhythm: 1101101011010 :: ok
Euclidean( 9, 13) -> Rhythm: 1110110110110 :: ok
Euclidean( 10, 13) -> Rhythm: 1111011101110 :: ok
Euclidean( 11, 13) -> Rhythm: 1111110111110 :: ok
Euclidean( 12, 13) -> Rhythm: 1111111111110 :: ok
Euclidean( 1, 14) -> Rhythm: 10000000000000 :: ok
Euclidean( 2, 14) -> Rhythm: 10000001000000 :: ok
Euclidean( 3, 14) -> Rhythm: 10001000010000 :: ok
Euclidean( 4, 14) -> Rhythm: 10010001001000 :: ok
Euclidean( 5, 14) -> Rhythm: 10100100100100 :: ok
Euclidean( 6, 14) -> Rhythm: 10101001010100 :: ok
Euclidean( 7, 14) -> Rhythm: 10101010101010 :: ok
Euclidean( 8, 14) -> Rhythm: 11010101101010 :: ok
Euclidean( 9, 14) -> Rhythm: 11011011011010 :: ok
Euclidean( 10, 14) -> Rhythm: 11101101110110 :: ok
Euclidean( 11, 14) -> Rhythm: 11110111101110 :: ok
Euclidean( 12, 14) -> Rhythm: 11111101111110 :: ok
Euclidean( 13, 14) -> Rhythm: 11111111111110 :: ok
Euclidean( 1, 15) -> Rhythm: 100000000000000 :: ok
Euclidean( 2, 15) -> Rhythm: 100000010000000 :: ok
Euclidean( 3, 15) -> Rhythm: 100001000010000 :: ok
Euclidean( 4, 15) -> Rhythm: 100100010001000 :: ok
Euclidean( 5, 15) -> Rhythm: 100100100100100 :: ok
Euclidean( 6, 15) -> Rhythm: 101001010010100 :: ok
Euclidean( 7, 15) -> Rhythm: 101010101010100 :: ok
Euclidean( 8, 15) -> Rhythm: 110101010101010 :: ok
Euclidean( 9, 15) -> Rhythm: 110101101011010 :: ok
Euclidean( 10, 15) -> Rhythm: 110110110110110 :: ok
Euclidean( 11, 15) -> Rhythm: 111011101110110 :: ok
Euclidean( 12, 15) -> Rhythm: 111101111011110 :: ok
Euclidean( 13, 15) -> Rhythm: 111111101111110 :: ok
Euclidean( 14, 15) -> Rhythm: 111111111111110 :: ok
Euclidean( 1, 16) -> Rhythm: 1000000000000000 :: ok
Euclidean( 2, 16) -> Rhythm: 1000000010000000 :: ok
Euclidean( 3, 16) -> Rhythm: 1000010000100000 :: ok
Euclidean( 4, 16) -> Rhythm: 1000100010001000 :: ok
Euclidean( 5, 16) -> Rhythm: 1001001001001000 :: ok
Euclidean( 6, 16) -> Rhythm: 1010010010100100 :: ok
Euclidean( 7, 16) -> Rhythm: 1010101001010100 :: ok
Euclidean( 8, 16) -> Rhythm: 1010101010101010 :: ok
Euclidean( 9, 16) -> Rhythm: 1101010110101010 :: ok
Euclidean( 10, 16) -> Rhythm: 1101101011011010 :: ok
Euclidean( 11, 16) -> Rhythm: 1110110110110110 :: ok
Euclidean( 12, 16) -> Rhythm: 1110111011101110 :: ok
Euclidean( 13, 16) -> Rhythm: 1111101111011110 :: ok
Euclidean( 14, 16) -> Rhythm: 1111111011111110 :: ok
Euclidean( 15, 16) -> Rhythm: 1111111111111110 :: ok |
_________________
Jan
also .. could someone please turn down the thermostat a bit.
|
|
|
Back to top
|
|
|
jazzmonster
Joined: Jun 29, 2014
Posts: 6
Location: Dublin, Ireland
|
| Posted: Mon Jun 30, 2014 2:39 pm Post subject:
|
|
|
| Blue Hell wrote: | Ok .. here is a variation that lets patterns start with a 1 always.
| Code: | function EuclideanRhythm3( aPulses, aSteps: Integer): string;
var
Error : Integer;
i : Integer;
begin
Result := '';
if aSteps > 0
then begin
Error := 0;
for i := 0 to aSteps - 1
do begin
Error := Error + aPulses;
if Error > 0
then begin
Result := Result + '1';
Error := Error - aSteps;
end
else Result := Result + '0';
end;
end;
end;
|
|
Thank's for this, it works great. It still isn't perfect as it doesn't start the rhythm on the correct onset, but as you say it is just a permutation. I can't get my head around why this is the case. Anyway, it's good enough and once the rhythms are playing they sound great. I really appreciate your help.
ChucK version:
| Code: | fun int[] euclideangenerator ( int pulses, int steps ) {
// Euclidean rhythm generator based Bresenham's algorithm
// pulses - amount of pulses
// steps - amount of discrete timing intervals
int seq[steps];
int error;
for ( int i; i < steps; i++ ) {
error + pulses => error;
if ( error > 0 ) {
true => seq[i];
error - steps => error;
} else {
false => seq[i];
}
}
return seq;
}
|
_________________
jazzmonster |
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Mon Jun 30, 2014 2:46 pm Post subject:
|
|
|
Thanks for bringing up the subject!
I finally found a nice algorithm to get it into my own soft synth 
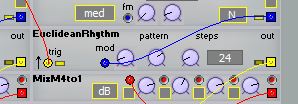
Added a pattern modulation input for fun.
_________________
Jan
also .. could someone please turn down the thermostat a bit.
|
|
|
Back to top
|
|
|
dutchsonoguy
Joined: Jul 03, 2014
Posts: 1
Location: Netherlands
|
| Posted: Thu Jul 03, 2014 7:06 am Post subject:
|
|
|
I actually posted a Euclidean rhythm class generator for chuck a little while a go at my website, maybe you find it useful:
http://www.casperschipper.nl/v2/uncategorized/euclidian-rhythms-in-chuck/
| Code: | class Euclid {
int bitmap[];
int remainder[];
int count[];
fun void buildString (int level) {
if (level == -1) {
append(bitmap,0);
} else if (level == -2) {
append(bitmap,1);
} else {
for (0 => int i; i <count> int divisor;
null @=> remainder;
null @=> count;
null @=> bitmap;
int a[100] @=> remainder;
int b[100] @=> count;
int c[0] @=> bitmap;
numPulses => remainder[0];
0 => int level;
do {
divisor / remainder[level] => count[level];
divisor % remainder[level] => remainder[level + 1];
remainder[level] => divisor;
level++;
} while (remainder[level] > 1);
divisor => count[level];
buildString (level);
}
fun int [] compute(int slots,int pulse) {
computeBitmap(slots,pulse);
return bitmap;
}
fun int [] append (int input[],int value) {
input.size() => int size;
size + 1 => input.size;
value => input[size];
return input;
}
fun void [] print () {
chout <= "Euclid pattern =" <= IO.newline();
for (int i;i<bitmap.size();chout <= bitmap[i++] <= " ") {
// nothing
}
chout <= IO.newline();
}
}
class TestEuclid { // this is a little testclass...
Euclid myPattern;
chout <= myPattern.toString() <IO> freq;
myPattern.compute(numSlots,pulses); // make a pattern with 15 slots of which 4 are turned on.
myPattern.print();
spork ~ schedule();
}
fun void ping(float gain,dur dura) { // a simple pulse
SinOsc c => Envelope e => Pan2 p => dac;
Math.random2f(-1,1) => p.pan;
.12 => e.gain;
freq => c.freq;
gain => c.gain;
e.value(1);
e.target(0);
dura * 2 => e.duration => now;
}
fun void schedule() { // sequencer
0 => int i;
myPattern.print();
while(1) {
spork ~ ping(myPattern.bitmap[i++],.1::second);
i % myPattern.bitmap.cap() => i;
.12::second => now;
}
}
}
TestEuclid test[10];
test.cap() => int i;
while(i--) { // 10 test patterns with random amount of slots and pulses, random harmonic of 55 hz.
// note: handpicking the values can give even nicer results
test[i].init(Math.random2(7,21),Math.random2(2,7),Math.random2(1,8)*110);
}
hour => now; |
|
|
|
Back to top
|
|
|
jazzmonster
Joined: Jun 29, 2014
Posts: 6
Location: Dublin, Ireland
|
| Posted: Fri Jul 04, 2014 5:08 am Post subject:
|
|
|
Thanks for this!
The code you posted here seems to have some lines missing close to the beginning compared to the code on your website.
The code from your website is giving an error message:
| Code: | [euclid.ck]:line(53): arguments type(s) do not match:
[euclid.ck]:line(53): ... for function 'int[].size(...)' ...
[euclid.ck]:line(53): ...(please check the argument types)
[euclid.ck]: ...in function 'append'
|
I'll see whether I can fix it.
Thanks again.
UPDATE: ok I realised I had an older version of chuck. It works great now!
_________________
jazzmonster |
|
|
Back to top
|
|
|
kingcrabmeat
Joined: Sep 04, 2014
Posts: 4
Location: US and A
|
| Posted: Tue Sep 09, 2014 9:18 am Post subject:
|
|
|
Final Edit: It pains me to give up on the problem of rectifying a computer-generated Euclidean rhythm to start at the first onset. After numerous failed approaches, I have determined that there is simply no elegant solution that I can find. It shouldn't be impossible, of course, but it is probably a nightmare to implement in code.
With that, I am thoroughly impressed by the efficacy of Bresenham's line algorithm and thankful that it was brought to light. It seems to me that the Bjorklund algorithm is comparatively less relevant in the context of generating Euclidean algorithms. The Bresenham line algorithm is far less complicated and produces qualitatively equal results as the Bjorklund algorithm.
Perhaps, one day, Euclid will reveal the answer to me in a dream. If that happens, I will tattoo it to my body and post pictures for everyone to see. |
|
|
Back to top
|
|
|
aggaz
Joined: Dec 29, 2014
Posts: 1
Location: Italy
|
Posted: Mon Dec 29, 2014 4:07 pm Post subject:
 Another implementation |
|
|
Dear chuckers,
I am learning chuck in these days, and just found this post.
Some time ago I was reading about euclidean patterns, and found an interesting PureData patch for their generation (this one http://www.pdpatchrepo.info/hurleur/euclid.pd).
As an exercise, I just ported it.
This is the result:
| Code: |
/* generates euclideian patterns
c: current step number
k: hits per bar
n: bar length
r: rotation
returns 1 or 0 according to the euclidean pattern*/
fun int euclide( int c, int k, int n, int r ) {
return (((c + r) * k) % n) < k;
}
0 => int i;
while(i < 12) {
euclide(i, 7, 12, 4) => int e;
//declaring b just to print e
<<<e>>> => int b;
1 +=> i;
100::ms => now;
}
|
The output seems reasonable to me.
Please note that it is possible to change the position in the pattern (rotation, variable r), and I am posting a code with parameters tuned to generate the output you were talking about in the first post.
Bye
-aggaz |
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Mon Dec 29, 2014 4:46 pm Post subject:
|
|
|
when that works it's brilliantly compact!
Will test it later.
and aggaz
_________________
Jan
also .. could someone please turn down the thermostat a bit.
|
|
|
Back to top
|
|
|
blue hell
Site Admin
Joined: Apr 03, 2004
Posts: 24388
Location: The Netherlands, Enschede
Audio files: 296
G2 patch files: 320
|
| Posted: Sat Jun 27, 2015 12:48 pm Post subject:
|
|
|
Just found out today that there is a direct relation to Walsh functions .. and reading back .. the relation to binary rate multipliers was not mentioned here yet.
Not sure how this would be handy for a ChucK implementation, but it seemed interesting enough to mention it.
_________________
Jan
also .. could someone please turn down the thermostat a bit.
|
|
|
Back to top
|
|
|
PHOBoS
Joined: Jan 14, 2010
Posts: 5792
Location: Moon Base
Audio files: 709
|
| Posted: Sun Jun 13, 2021 4:10 am Post subject:
Re: Another implementation |
|
|
I needed to create some euclidean sequences for an experiment so was looking up the code and stumbled upon this.
| aggaz wrote: | | Code: |
/* generates euclideian patterns
c: current step number
k: hits per bar
n: bar length
r: rotation
returns 1 or 0 according to the euclidean pattern*/
fun int euclide( int c, int k, int n, int r ) {
return (((c + r) * k) % n) < k;
}
|
|
That is absolutely brilliant indeed! 
It's how I imagine people that can actually write some proper code do stuff all the time.
thank you very much for posting this.
_________________
"My perf, it's full of holes!"
http://phobos.000space.com/
SoundCloud BandCamp MixCloud Stickney Synthyards Captain Collider Twitch YouTube |
|
|
Back to top
|
|
|
|
Forum index » DIY Hardware and Software » ChucK programming language
FAQ
Calendar
Search
Memberlist
Usergroups
Register
Profile
Log in to check your private messages
Log in
Chat Room
