 Dedicated to experimental electro-acoustic and electronic music
Dedicated to experimental electro-acoustic and electronic music
|
Articles / The Soundwave-From Organs To Nyquist
The Soundwave - from Organs to Nyquist
Note: this article was originally written by someone who does not speak english as a first language. If you find anything that you know is grammatically wrong, or sentences that were built in a weird way, feel free to just dive in and correct. Thanks. In this article we will look at the soundwave in relation to the history of synthesizers. We will compare common two dimensional representations of soundwaves with their actual sounds, why they look like they do and how they may be treated and created. All of this will lead up to issues when producing sound digitally, and what Nyquist is all about. The SoundWave
Sound happens when waves of compressed air enters the ear. The waves that we hear are small and quick, more like an itch than something that thunders in from the sea and hits the beach. Sound can originate in many ways, some is brought on as the planet stirs air around (weather), some is made by massive structures moving, some is made when some point source vibrates, exciting the air around it. Often there will be a lot of this going on, creating sound from many places at once. The ear - with its sophisticated mechanisms for analysing vibrations - is good at sorting out various sources of sound, sensing that a bucket hit the ground or lightning struck somewhere. With two ears, a creature can figure out where the source of one specific sound was in the world around it.  The sound of a tone passing around and inside an ear One type of sound that the ear is especially keen on hearing is the steady, regular beating of air that we call tones. Humans will percieve waves as tones when their frequency surpasses 20 Hz, meaning that a wave of compressed air hits the eardrum more than twenty times per second. The ear is able to sense several separate tones happening at the same time, as when an orchestra with many instruments plays a song. Tones that enter the air will usually not be smooth or uniform; they will have structure. The ear is good at discerning these structures - or timbres - in fine detail. If we want to study these structures, it makes sense to try to make a visual representation of the waves that enter our ear. The examples above aren't very clear though, as it's hard to see the structure of waves in the various shades of gray. A better visualization is to draw a curve of the air density at a specific point in space (inside the ear), over time.  Representations of irregular and regular waveforms, representing pressure using shades of grey (top) and two-dimensional curves (bottom) This kind of curve is what we usually see when talking about waveforms, looking at oscilloscopes or working with software synthesizers. Sometimes it can be good to remember that we're looking at something that represents the state of something over time (as a transverse wave) whereas what actually happens in the world is a complex system of waves of pressure (longitudinal waves). Additive Synthesis
Note: i don't really know that much about organs and other things here, so I'm guessing a lot. If someone who knows better finds errors here, feel free to correct them. If the whole premise of my reasoning around organs and timbre is wrong, please add a comment about that here The pipe organ is an old concept, dating back to ancient Greece in the third century BC. The general principle in larger organs is to take simple tones - created by blowing wind into ranks of pipes - and combine them to create different timbres. For example an organ might have two ranks of pipes: rank A and rank B. Using organ stops, you can turn each rank on or off, enabling three timbres: rank A by itself, rank B by itself, and rank A and B together. 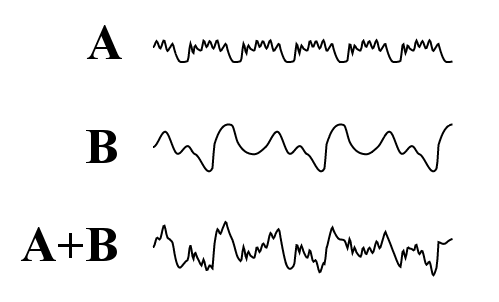 Two regular waveforms and a third waveform which is the sum of the other two This is an example of additive sound synthesis - adding several tones to create a new tone, or to put it another way: adding several timbres to create a new timbre. Moving on to modern times, after electricity arrived, people found that you could create an organ-like sound using tonewheels, a construction where spinning wheels generated pulses of electric current that, when amplified, played tones through a loudspeaker. The principle of having stops that turned ranks of tones on and off was inherited from the old mechanical organs, into these electronic organs. One interesting exercise you can do with a synthesizer is to set oscillators to play sine waves (or, in the absence of sine waves, triangle waves), octaves apart. You can easily do a good impression of an electronic organ this way. If you have access to many oscillators per voice, you can get a half decent church organ. This shows how the concept of additive synthesis is still available and useful, and how the legacy of organs still lives in our modern instruments. It also makes us notice the sine wave. So what is a sine wave, and what's so special about it? The Sine Wave
The sine function is a model for describing fundamental oscillation. A sine wave can be shown as a curve where y is the value of sine for x. 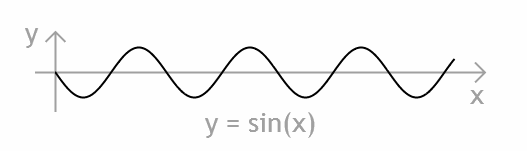 A graph of the sine function One use of this model is that all oscillations can be described as a sum of sine waves at different frequencies and amplitudes. As we saw above, this works for the output of an organ; the tones in our exercise were literally built out of sine waves. It also works for sounds like the chaotic rumble of the lowest keys on a piano, or a hoarse blues singer. For the last we would need a large amount of sine waves and an outrageous amount of work, but theory says it can be done. The frequencies of the sine waves needed to create a specific timbre are called the fundamental and the overtones. The fundamental is the lowest frequency amongst the sine waves, and the overtones make up the remaining frequencies, all higher than the fundamental. The sine function describes different kinds of phenomena around us: the vertical position of a point on the edge of a freely spinning wheel, or a weight bouncing at the end of a spring. If you hop on a spaceship, ride out to a neighbouring solar system, look back here and through some marvel of technology measure the planet Jupiter's position in relation to the Sun over time, that will be a sine wave. Interactive demonstration of how a spinning wheel relates to the sine wave One application of additive synthesis is to use large banks of sine oscillators to create complex timbres - tens or hundreds of oscillators tuned to any kinds of relative frequencies, not just octaves apart. Another step is then to make machines that analyse sounds, calculate the frequencies of sine tones that make them up, and then recreate them using additive synthesis that can be treated and tweaked. Another use is to get around the problem with aliasing in digital synthesis, but we're getting ahead of ourselves... Subtractive Synthesis
With subtractive sound synthesis, you start with complex waveforms and then work to remove frequencies (or overtones or harmonics as they may also be called.) This is done by sending the sound through various kinds of filters. A filter in this context is a system that lets selected intervals of frequencies pass through it, while others are removed at the output (filtered out.) A common kind is the lowpass filter, which removes frequencies that are above some threshold value that has been set for the filter. A lowpass filter with its threshold set to 4000 Hz would keep all harmonics below that frequency (e.g. 200 Hz or 1500 Hz), but erase harmonics above (e.g. 6000 Hz or 100000 Hz). This works the opposite way compared to additive synthesis, where you add frequencies rather than remove them. After learning about additive synthesis, subtractive synthesis feels destructive and careless in a way; all those painstakingly combined frequencies that you added with your tonewheels and pipes, to just throw them away. The reality is that overtones are cheap and everywhere. Observe the sawtooth or ramp waveform: 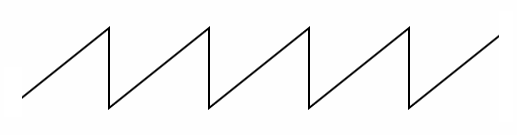 A sawtooth waveform The way to create this simple waveform using additive synthesis is well-known: it is the sum of a series of sinewaves, all multiples of the fundamental, with decreasing amplitude. Interactive demonstration of how to construct a sawtooth by adding sinewaves or harmonics. That's a lot of harmonics to piece together. An alternative way in analog electronics, is to set up a mechanism that lets a voltage drop steadily at an output, until it hits the lower amplitude boundary, at which point the mechanism resets to the upper amplitude boundary and falls again. Interactive demonstration of a sawtooth being drawn using a simple value drop/reset technique As it turns out, in analog sound synthesis, creating a sawtooth oscillator using the latter technique is far cheaper than creating an oscillator that outputs a single sinewave. It's a shortcut to a waveform that is rich in harmonics, without having to worry about sinewaves at all. The sawtooth through the lowpass filter has also been responsible for a substantial amount of synthesizer music that you have probably heard - it's one of the most classic synth sounds. You need to filter it though, because the overtones go so high up it's painful to listen to in its pure form. Comparing with additive synthesis, it's easy to see the benefits in the subtractive kind. There are waveforms around that sound nice (after having been treated with filters), and may be obtained cheaply using simple electronic circuits. Adding sinewaves together gives you precise control over the sound you create, but involves massive complicated circuits with challenging interfaces. You will want ways to control the pitch and amplitude of each oscillator, which means many knobs for the additive kind, whereas a sawtooth is just one oscillator, which goes a long way in comparison, and is simpler to control. Digital Synthesis
TODO: Relate back to additive synthesis and talk about how overtones cross the Nyquist frequency and mess things up. Talk about Nyquist and aliasing, pulse trains. An alternative to creating dedicated electronic circuits for generating sound is to have a computer do it instead, generating the sound digitally. One way to do this is to play samples. You can look at a sample waveform as a series of voltages that are sent in quick succession to an audio output. If there are enough samples and they are played quickly enough, we can generate any kind of sound. The sample waveform may have been created from a recording or some computer algorithm. 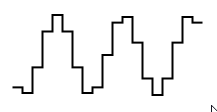 A sample of a sinewave with visible resolution/carrier wave Looking at the image on the side here, one issue might come to mind. Instead of the smooth sine waves we have seen before, this one - though clearly giving the impression of a sine wave - looks flawed with its edges and squarish plateauxs. Won't that have an impact on the sound? The answer is that it depends on how fast the waveform is playing. The human ear is limited to hearing frequencies up to somewhere around 20.000 Hz, or 20 kHz (small children or people with super-hearing may sense tones that reach 20 kHz, most of us have to settle for lower).If the interval between each sample (the width of each stack in the sine wave sample above), is, say, a hundredth of a second, meaning that samples are played at frequency of 100 Hz (called a carrier frequency or carrier wave), then that frequency will be in the audible range and we can hear it - this phenomenon is called aliasing. If it is played at 20 kHz (meaning 20000 samples are played every seconds), then we won't be able to hear it for this waveform - it will be smooth enough. 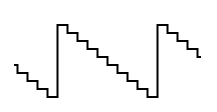 A sample of a sawtooth waveform with visible carrier wave Another way to generate sound digitally is to have the computer calculate the waveform on the fly. A sawtooth waveform could then be created using a simple series of "for" loops. For those of you who aren't programmers, a for loop is mechanism for doing the same thing over and over again, in iterations. A sawtooth waveform can be generated by starting with a value, for example 10, then subtracting one from it over and over again until it reaches zero, at which point we reset the value to 10 and start the loop again. At each iteration, after we subtract one, we output the current value as a voltage on the audio output. Do it quickly enough, and we get an audible sawtooth waveform. Again, we see something that we can deduce as being a sawtooth waveform, but an imperfect one, with edges and plateauxs. For the sampled sinewave above, I argued that you will hear the carrier frequency if it's too low, but if you set it at 20000 Hz you're ok. Will that reasoning hold here as well? It turns out that it's not that easy in this case. If you have access to a programming language like ChucK, or a synthesizer with wavetable technology, you can try this yourself as an experiment. If you play a sawtooth sample or computer-generated sawtooth waveform, the higher notes will sound distorted and strange, with a weird pulsating effect. To explain what's going on here, we need to look at ice cream sales. Statistics Concerning Ice Cream Sales
Just before you reach the beach in Falsterbo - a small town at the southern tip of the Swedish coast which is a popular place in the summer - there's a tiny ice cream stand called "Nisses Glass". It may not look like much, but it's a proud establishment which has been there a long time, at least since the early 1900s. Nisse (the owner) got it into his head at some point that he wanted to keep better statistics on the ice cream sales. There was a long log from sales measured over one day every april 10 which showed an irregular but fairly flat curve. Nisse was worried that this log wasn't useful; stock would run out every now and then and he had a hunch that there may be busier days than april 10 over the course of one year. He decided that he would start measuring sales more often. Because of practical issues and laziness, the plan he came up with was to measure the sales over one week every seven months. That way he would see if there were more sales at other parts of the year. After a decade or so he had some data to work with. [Image of sales curve based on every seventh month] It was clear early on that there were indeed more sales at other points of the year, and Nisse made sure that stock was increased. The new problem was that sometimes stock would perish because Nisses Glass didn't make enough sales. He wondered if there might be a pattern to the sales, but the curve looked pretty random. Nisse decided to up the sample frequency to one week every five months. Extra work, but hopefully something would come out of it. [Image of sales curve based on every fifth month] Unfortunately it didn't: it was all still a random mess. Nisse gave up, he was getting old and retired to his beautiful villa down near Falsterbo beach, handing over Nisses Glass to his son, Hasse. Being young and full of energy, Hasse decided to try to beat his dad's statistical adventure by measuring sales over one week every single month. It paid off - he didn't need long to see a clear pattern emerging [Image of sales every month] The curve told a clear message: sales were low between october and march, and ramped up during the summer. With hindsight, Hasse could piece together a theory as to how this worked. People liked eating ice cream during the summer because it was warm, and they also liked going to the beach and would pass by Nisses Glass on the way there. In the winter people weren't so keen on going to the beach, especially if the water was frozen and difficult to swim in, and they would rather eat or drink something warm than eat cold ice cream. By now I guess you have realized that this whole example is fictional - there never was any Nisses Glass and people aren't really that stupid, not even in Falsterbo. This thought experiment serves to illustrate how aliasing messes things up when it comes to sampling. What has ice cream got to do with anything?!
Ice creams sales fluctuate regulary at Nisses Glass, at a fundamental frequency of one year. The mathematical tools that exist to analyse oscillations like this are usually used to observe tiny waves as in radiowaves or sound, but some of the theory is hinted at in the example above. One of the principles in sound analysis is that, in order to determine a frequency within a set of sampled data, you need to have sampled at least twice as often as the wavelength of the frequency you want to determine. So if you want to determine an oscillation that completes one cycle in one second, you need to register at least two samples in one second for that oscillation to become apparent. In other terms, if you are trying to detect a frequency at 1 Hz in a sample set, you need to have gathered samples at at least 2 Hz (i.e. with a carrier frequency of 2 Hz) - twice as fast. That's a lazy illustration of something called the Nyquist-Shannon sampling theorem. Half the carrier frequency (i.e. the maximum frequency that can be detected in the data set) is called the Nyquist frequency (which I will refer to as Nyquist in the rest of this article) after a guy called Harry Nyquist who worked with transmitting information via telegraph in the early 1900s. For a sample set with a carrier frequency of 2 Hz, Nyquist is at 1 Hz. So why did the sample from every five months look as messy as the one for seven months? The problem there is overtones. What I've stated in the previous couple of paragraphs isn't the whole story - if the target frequency is close to Nyquist you will only be able to detect it as long as it is a pure sinewave. If the waveform has a different shape, as in the ice cream curve or the sawtooth wave, it can be broken down into a fundamental and its overtones. If the fundamental is close to the Nyquist frequency that means that its overtones will go above Nyquist, and can't be properly represented in the sample set. They won't disappear into thin air though, each overtone will rather appear as some other frequency, lower than Nyquist. Like this: [Big image of ice cream curve broken into harmonics, the aliased version of each harmonic and a sinewave representation of the aliased version] This explains why the five month frequency didn't work very well for Nisse, the overtones of the non-sinelike oscillation appeared as phantom frequencies in the data, obscuring the interesting data. It also illustrates the problem with recreating a sawtooth waveform by using simple programming loops. [Similar image to the ice cream curve example above, but with a sawtooth instead] This also shows what the ear is hearing when a sawtooth is playing on inadequate sample rates. Additive synthesis to the rescue
I though I'd go full circle by illustrating how the problem with aliasing and overtones appearing as phantom frequencies can be solved using additive synthesis. I mentioned earlier that additive synthesis is expensive to implement using electronics in comparison to e.g. sawtooth oscillators. For a computer program it's a different story. A program will run on a processor with some memory attached. Using a lookup table (stored in memory) and interpolation you can do a good impression of a sinewave with little processing cost, especially when the frequency is in the upper range (if the frequency is low enough you can use the crude way to reproduce it, since audible overtones stay below Nyquist). If you set up a handful of sinewave oscillators with appropriate relative frequencies and amplitudes, and omit the overtones that you can't reproduce (i.e. they're above Nyquist), you can build your complex waveform just like with the old pipes and tonewheels. [Image of sawtooth, its overtones with frequencies indicated, and indications of which overtones go above Nyquist] There are other, more effective, ways to work your way around aliasing, but there are solutions that using multiple sinewaves like above. If you feel like experimenting with additive synthesis, it can be useful to know what happens to harmonics when you cut them into samples, and how you can rebuild them. Something to ponder the next time you jam on your local church organ. |
Edit - History - Print - Recent Changes - Search Page last modified on 2013-03-17 15:33 [UTC-7] - 526 views